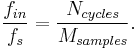Coherent sampling
Fast Fourier Transform (FFT) is a common tool to investigate performance of for data converters and other sampled systems. Coherent sampling refers to a certain relationship between input frequency, 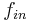 , sampling frequency,
, sampling frequency, 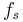 , number of cycles,
, number of cycles, 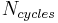 , in the sampled set and number of samples,
, in the sampled set and number of samples, 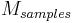 . With coherent sampling one is assured that the signal power in an FFT is contained within one FFT bin, assuming single input frequency.
. With coherent sampling one is assured that the signal power in an FFT is contained within one FFT bin, assuming single input frequency.
The condition for coherent sampling is given by
If we have 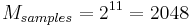 and
and 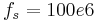 and we want an input frequency close to
and we want an input frequency close to 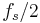 , let's say
, let's say 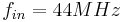 , then
, then 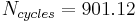 which is close to an integer, so we could round it down to
which is close to an integer, so we could round it down to 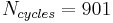 and we would get
and we would get 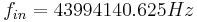 . This is an input frequency that satisfies coherent sampling and makes sure that we get an integer number of cycles.
. This is an input frequency that satisfies coherent sampling and makes sure that we get an integer number of cycles.
This integer number should be chosen carefully. We have three possible types of integers, even, odd, and prime. Even is not a good idea since we would hit the same code every M samples, where M can be much less than N. Odd is a better idea since it takes longer to hit the same code. According to some sources [1] a prime number of cycles is the best (with the exception of the prime 2) because it takes a long time before the same code repeats.